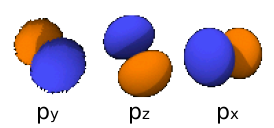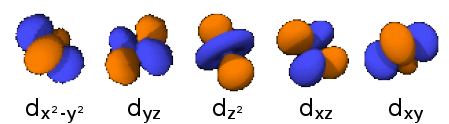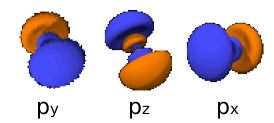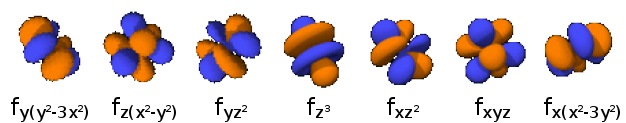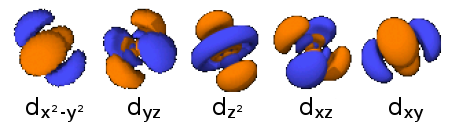Γενική και Ανόργανη Χημεία/Ατομική δομή

Δυαδική φύση του φωτός

Επί πολλούς αιώνες το φως και η ικανοποιητική επιστημονική εξήγηση της φύσης του αποτέλεσε μέγα αίνιγμα και πεδίο διαμάχης ανάμεσα στους επιστήμονες. Κατά τον 17^ο αιώνα, η διαμάχη κορυφώθηκε ανάμεσα στις σχολές των αυθεντιών της εποχής, του Ισαάκ Νεύτων και του Κρίστιαν Χόυχενς. Είναι ροή υλικών σωματιδίων ή κύμα = ενέργεια; Διαδίδεται ευθύγραμμα, ανακλάται, διαθλάται, μεταδίδει ορμή σε σώματα πάνω στα οποία προσκρούει, σαν υλικό σώμα και ταυτόχρονα, δίνει φαινόμενα περίθλασης και συμβολής, σαν κύμα.
Το ορατό φως αποτελεί ένα μικρό τμήμα του ηλεκτρομαγνητικού φάσματος, που περιλαμβάνει επίσης (αλλά όχι μόνο) τις ακτίνες Χ, την υπέρυθρη και την υπεριώδη ακτινοβολία.
Η ταχύτητα του φωτός στο κενό είναι σταθερή ($c\simeq 3\cdot 10^{8}\;m/s$), ανεξάρτητη από τη συχνότητά του (v) ή το μήκος κύματός του (λ).
Από τα τελευταία χρόνια του 19^ου αιώνα παρατηρήθηκε το «φωτοηλεκτρικό φαινόμενο», δηλαδή το φαινόμενο να αποσπούνται ηλεκτρόνια από μέταλλα όταν πέφτει πάνω σ' αυτά φως με επαρκή συχνότητα, άρα και ενέργεια, η οποία όμως εξαρτάται και από την ένταση της φωτεινής ακτινοβολίας.

Το 1905 ο Άλμπερτ Αϊνστάιν επέκτεινε την υπόθεση του Μαξ Πλανκ θεωρώντας την ηλεκτρομαγνητική ακτινοβολία «κβαντισμένη», δηλαδή αποτελούμενη από διακριτά τμήματα που λέγονται «κβάντα». Στα κβάντα φωτός έδωσε το όνομα «φωτόνια». Διατύπωσε λοιπόν την παρακάτω σχέση:

$E=hv$

όπου:

Ε: ενέργεια φωτονίου.

$h=6,6\cdot 10^{-34}\;Js:$ «Σταθερά του Planck».

v : συχνότητα ηλεκτρομαγνητικής ενέργειας.

Η σχέση αυτή προς τιμή και των δυο ερευνητών ονομάστηκε «σχέση Planck - Einstein». Η ερμηνεία του φωτοηλεκτρικού φαινομένου με αυτήν είναι απλή: Η κινητική ενέργεια κάθε αποσπούμενου ηλεκτρονίου δίνεται από την ακόλουθη σχέση:

$hv=A+{\frac {1}{2}}m\upsilon ^{2}$

όπου:

$h=6,6\cdot 10^{-34}\;Js:$ «Σταθερά του Planck».

v : συχνότητα ηλεκτρομαγνητικής ενέργειας.

Α : σταθερά που εξαρτάται από χαρακτηριστικά της μεταλλικής επιφάνειας.

$m=m_{e}=9,1\cdot 10^{-31}\;m:$ μάζα ηρεμίας ηλεκτρονίου.

υ : ταχύτητα ηλεκτρονίου.

Για ένα σωματίδιο με μάζα m₀ η ορμή (p) δίνεται από την ακόλουθη σχέση:

$p={\frac {\sqrt {E^{2}-{m_{0}}^{2}c^{4}}}{c}}$

όπου:

p: η ορμή.

E: η κινητική ενέργεια.

m₀: μάζα ηρεμίας του σωματιδίου.

$c=3\cdot 10^{8}\;m/s:$ Η ταχύτητα του φωτός στο κενό.

Για ένα φωτόνιο, για το οποίο θεωρείται ότι m₀ = 0, η παραπάνω σχέση γίνεται:

$p={\frac {E}{c}}={\frac {hv}{c}}={\frac {h}{\lambda }}$

όπου:

p: η ορμή.

E: η κινητική ενέργεια.

$c=3\cdot 10^{8}\;m/s:$ Η ταχύτητα του φωτός στο κενό.

$h=6,6\cdot 10^{-34}\;Js:$ «Σταθερά του Planck».

v : συχνότητα ηλεκτρομαγνητικής ενέργειας.

λ : μήκος κύματος ηλεκτρομαγνητικής ενέργειας.

Η παραπάνω σχέση είναι γνωστή ως «σχέση υλοκυμάτων του de Broglie». Με αυτήν διατυπώνονται ότι υπάρχει δυαδική (υλική και ενεργειακή) φύση και στην ύλη και στα ηλεκτρομαγνητικά κύματα.

Ατομικά Τροχιακά

Η εξίσωση Schrödinger

Η Κλασσική Μηχανική της Φυσικής βασίζεται σε ορισμούς όπως π.χ.: «Δύναμη ονομάζεται ο ρυθμός μεταβολής της ορμής», ή μαθηματικά:

${\vec {F}}={\frac {d{\vec {p}}}{dt}}$

όπου:

${\vec {F}}$: η δύναμη.

${\vec {p}}$: η ορμή.

t: ο χρόνος.

Είναι ένα αξίωμα που γενικά ισχύει στα υλικά σώμτα του μακρόκοσμου, αλλά δεν μπορεί να χρησιμοποιηθεί με ικανοποιητική ακρίβεια στα υλοκύματα του μικροκόσμου. Βασικό κριτήριο εφαρμογής ή μη είναι η συμφωνία, προσέγγιση ή διαφωνία με τα πειραματικά δεδομένα. Για την εξέταση του μικρόκοσμου θα μπορούσαμε να εφαρμόσουμε δυο μεθόδους;

1. Να δοκιμάσουμε την αξιοπιστία διαφόρων αξιωμάτων από την αρχή, μέχρι να βρούμε κάποιο που να προσεγγίζει τα πειραματικά δεδομένα.

2. Να τροποποιήσουμε τα αξιώματα της Κλασσικής Φυσικής στις συνθήκες των υλοκυμάτων, μέχρι να βρούμε κάποιο που να προσεγγίζει τα πειραματικά δεδομένα.

Ο δεύτερος τρόπος φαίνεται πιο απλός και επομένως θα τον ακολουθήσουμε παρακάτω. Σε πρώτη φάση αναζητούμε τα βασικά χαρακτηριστικά που χρειαζόμαστε για την εξίσωσή μας: Πρώτα απ' όλα χρειαζόμαστε μια κυματική εξίσωση, όπως αυτή που περιγράφει τις ταλαντώσεις της χορδής ενός βιολιού. Αλλά δεν μας ενδιαφέρει προς στιγμήν ο παράγοντας χρόνος, αλλά περισσότερα τα επιτρεπτά ενεργειακά επίπεδα στα διάφορα άτομα, ιόντα ή μόρια. Σ' αυτήν τη φάση δηλαδή δε χρειαζόμαστε παραγώγους ως προς το χρόνο. Περιμένουμε πάντωςνα δούμε τα αναμενόμενα από την Κλασσική Φυσική: κινητική ενέργεια των σωματιδίων και την έκφραση των έλξεων και των απώσεων, ηλεκτροστατικών και μαγνητικών, στη μορφή της δυναμικής ενέργειας των σωματιδίων. Τέλος περιμένουμε την ανάμιξη της σχέσης de Broglie (βλ. παραπάνω). Ας αρχίσουμε λοιπόν να γράφουμε μια τέτοια κυματική εξίσωση, περιορίζοντάς την, για αρχική απλούστευση σε μια διάσταση, μόνο στον άξονα x:

$y{\begin{pmatrix}x\end{pmatrix}}=A\eta \mu {\frac {2\pi x}{\lambda }}$

όπου:

$y{\begin{pmatrix}x\end{pmatrix}}$: το πλάτος της ταλάντωσης.

x: το μήκος της οριζόντιας διάδοσης του κύματος.

A: το μέγιστο πλάτος της ταλάντωσης, όταν $\eta \mu {\frac {2\pi x}{\lambda }}=1$.

• Σημειώστε ότι στην παραπάνω σχέση υποθέσαμε ότι η αρχή (σημείο 0) του άξονα x συμπίπτει με έναν από τους κόμβους της ταλάντωσης, δηλαδή ότι: $y{\begin{pmatrix}0\end{pmatrix}}=0$.

Τώρα παραγωγίζουμε δυο φορές κατά μέλη την παραπάνω εξίσωση, οπότε παίρνουμε:

${\frac {d^{2}y}{dx^{2}}}=-{\frac {4\pi ^{2}A}{\lambda ^{2}}}\eta \mu {\frac {2\pi x}{\lambda }}\Leftrightarrow {\frac {d^{2}y}{dx^{2}}}=-{\frac {4\pi ^{2}}{\lambda ^{2}}}y$

Η εξίσωση αυτή έχει απειρες λύσεις, γιατί δε θέτει κανέναν απολύτως περιορισμό για το Α. Επίσης, ούτε το λ περιορίζεται, εκτός από την τιμή 0, που έτσι κι αλλιώς δεν έχει φυσικό περιεχόμενο. Ωστόσο μια γενική λύση της παραπάνω εξίσωσης (δοκιμάστε την αν αμφιβάλετ) είναι η ακόλουθη:

$y{\begin{pmatrix}x\end{pmatrix}}=A\eta \mu {\begin{bmatrix}{\frac {2\pi }{\lambda }}{\begin{pmatrix}x+\phi \end{pmatrix}}\end{bmatrix}}$

όπου:

φ: γωνία φάσης.

Μπορούμε να περιορίσουμε την απροσδιοριστία που προκύπτει, θέτοντας πάλι: $y{\begin{pmatrix}0\end{pmatrix}}=0$, οπότε η παραπάνω σχέση γίνεται:

$A\eta \mu {\begin{bmatrix}{\frac {2\pi }{\lambda }}{\begin{pmatrix}0+\phi \end{pmatrix}}\end{bmatrix}}\Leftrightarrow \phi =0$

.

Έτσι ξανακαταλήγουμε όμως στην αρχική:

$y{\begin{pmatrix}x\end{pmatrix}}=A\eta \mu {\frac {2\pi x}{\lambda }}$

Ακόμη, μπορούμε να μειώσουμε κι άλλο τις δυνατές λύσεις, θεωρώντας αξιωματικά ότι σε ένα σημείο, έστω $\ell$, είναι: $y{\begin{pmatrix}\ell \end{pmatrix}}=0$. Στην περίπτωση αυτή παίρνουμε:

$y{\begin{pmatrix}\ell \end{pmatrix}}=A\eta \mu {\frac {2\pi \ell }{\lambda }}=0\Leftrightarrow {\frac {2\pi \ell }{\lambda }}=n\pi \Leftrightarrow \lambda ={\frac {2\ell }{n}}$

.

όπου:

n: ακέραιος αριθμός.

Ξεκινώντας δηλαδή από μια εξίσωση για ένα απλό κύμα, με πρότυπο τη χορδή ενός βιολιού, φτάσαμε ήδη στην πρώτη κβάνγτωση και στον κύριο κβαντικό αριθμό n. Η μετατροπή της παραπάνω σχέσης για τα υλοκύματα είναι απλή: Πρώτα απ' όλα αντικαθιστούμε το y με το ψ. Έπειτα χρησιμοποιούμε τη σχέση de Broglie για να αντικαταστήσουμε το μήκος κύματος (λ) με την ορμή του υλοκύματος στον άξονα x (p_x). Έτσι παίρνουμε την κυματοσυνάρτηση:

${\frac {d^{2}\psi }{dx^{2}}}=-{\frac {4\pi ^{2}}{h^{2}}}{p_{x}}^{2}\psi$

.

Όμως η παραπάνω εξίσωση δεν είναι έτοιμο, αφού δεν περιγράφει την επίδραση καμιάς δύναμης στο υλόκυμα. Περιγράφει απλά ένα υλοσωμάτιο που κινείται ελεύθερα σε μια ευθεία γραμμή. Ο μόνος τρόπος για να εισάγουμε τη δύναμη χωρίς να χρησιμοποιήσουμε το χρόνο είναι ως παράγωγο της δυναμικής ενέργειας που προκύπτει από την επίδρασή της. Η ορμή του σωματιδίου συνδέεται με την κινητική ενέργεια (T) νε την ακόλουθη σχέση:

$T={\frac {1}{2}}m\upsilon ^{2}={\frac {p^{2}}{2m}}$

.

όπου:

m: η μάζα του σωματιδίου.

Αλλά η Τ είναι η διαφορά της δυναμικής ενέργειας [V(x)], από την ολική ενέργεια (Ε). Άρα:

$T=E-V{\begin{pmatrix}x\end{pmatrix}}\Leftrightarrow {\frac {{p_{x}}^{2}}{2m}}=E-V{\begin{pmatrix}x\end{pmatrix}}\Leftrightarrow {p_{x}}^{2}=2m{\begin{bmatrix}E-V{\begin{pmatrix}x\end{pmatrix}}\end{bmatrix}}$

Αντικαθιστώντας τώρα το p_x στην κυματοσυνάρτηση από την παραπάνω, παίρνουμε:

${\frac {d^{2}\psi }{dx^{2}}}=-{\frac {8\pi ^{2}m}{h^{2}}}{\begin{bmatrix}E-V{\begin{pmatrix}x\end{pmatrix}}\end{bmatrix}}\psi \Leftrightarrow -{\frac {h^{2}}{8\pi ^{2}m}}{\frac {d^{2}\psi }{dx^{2}}}+V{\begin{pmatrix}x\end{pmatrix}}\psi =E\psi$

Επεκτείνοντας τώρα την παραπάνω εξίσωση στις 3 διαστάσεις του χώρου με άξονες x, y και z, παίρνουμε την «εξίσωση Schrödinger»:

$-{\frac {h^{2}}{8\pi ^{2}m}}{\begin{pmatrix}{\frac {\partial ^{2}\psi }{\partial x^{2}}}+{\frac {\partial ^{2}\psi }{\partial y^{2}}}+{\frac {\partial ^{2}\psi }{\partial z^{2}}}\end{pmatrix}}+V{\begin{pmatrix}x,y,z\end{pmatrix}}\psi =E\psi$

.

Η παραπάνω εξίσωση συχνά « συμμαζεύεται» με τη χρήση δυο τελεστών:

1. «Ανάδελτα τετράγωνο»: $\nabla ^{2}={\frac {\partial ^{2}\psi }{\partial x^{2}}}+{\frac {\partial ^{2}\psi }{\partial y^{2}}}+{\frac {\partial ^{2}\psi }{\partial z^{2}}}$, οπότε γίνεται:

$-{\frac {h^{2}}{8\pi ^{2}m}}\nabla ^{2}+V{\begin{pmatrix}x,y,z\end{pmatrix}}\psi =E\psi$

.

2. «Χάμιλτον»: $H=-{\frac {h^{2}}{8\pi ^{2}m}}\nabla ^{2}+V{\begin{pmatrix}x,y,z\end{pmatrix}}$, οπότε γίνεται:

$H\psi =E\psi$

.

Χαμιλτονιανή

Σύμφωνα με την « Αρχή της Αντιστοιχίας » του Bohr πρέπει να μπορούν να εφαρμοστούν οι κβαντικές εξισώσεις και στα μακροσκοπικά σώματα. Η συνολική συνάρτηση που παριστάνει την ολική ενέργεια ενός σώματος σε συνάρτηση με την ολική ορμή και δυναμική ενέργειά του λέγεται « συνάρτηση Hamilton » και αποδίδεται από τον τύπο:

$H_{f}={\frac {1}{2m}}{\begin{pmatrix}{p_{x}}^{2}+{p_{y}}^{2}+{p_{z}}^{2}\end{pmatrix}}+V{\begin{pmatrix}x,y,z\end{pmatrix}}$

όπου:

H_f: η συνάρτηση Hamilton.

m: η μάζα του σώματος.

p_x, p_y, p_z: η ορμή του σώματος αναλυμένη στους 3 άξονες του χώρου x,y,z.

V(x,y,z): η δυναμική ενέργεια του σώματος.

Είναι ολοφάνερη η αντιστοιχία μεταξύ του τελεστή και της συνάρτησης Hamilton. Αρκεί:

$p_{x}\rightarrow -{\frac {ih}{2\pi }}{\frac {\partial }{\partial x}}\Leftrightarrow {p_{x}}^{2}\rightarrow -{\frac {h^{2}}{4\pi ^{2}}}{\frac {\partial ^{2}}{\partial x^{2}}}$

• Ομοίως βέβαια και για τους άλλους άξονες.

Επίσης, αν έχουμε ένα σύστημα n σωμάτων ισχύουν αντίστοιχα:

$H_{f}=\sum _{i=1}^{n}{\begin{bmatrix}{\frac {1}{2m_{i}}}{\begin{pmatrix}{p_{x_{i}}}^{2}+{p_{y_{i}}}^{2}+{p_{z_{i}}}^{2}\end{pmatrix}}+V{\begin{pmatrix}x_{i},y_{i},z_{i}\end{pmatrix}}\end{bmatrix}}$
και
$H=-\sum _{i=1}^{n}{\begin{bmatrix}{\frac {h^{2}}{8\pi ^{2}m_{i}}}{\begin{pmatrix}{\frac {\partial ^{2}}{\partial {x_{i}}^{2}}}+{\frac {\partial ^{2}}{\partial {y_{i}}^{2}}}+{\frac {\partial ^{2}}{\partial {z_{i}}^{2}}}\end{pmatrix}}+V{\begin{pmatrix}x_{i},y_{i},z_{i}\end{pmatrix}}\end{bmatrix}}$

Η εξίσωση Schrödinger γράφεται για ένα τέτοιο σύστημα:

$H\psi =E\psi$

Οι λύσεις της ψ λέγονται « ιδιοσυναρτήσεις » και οι αντίστοιχες τιμές ενέργειας (Ε) « ιδιοτιμές ».

Η φυσική σημασία της κυματοσυνάρτησης

Η ψ, η κυματοσυνάρτηση ενός σωματιδίου (ή συστήματος σωματιδίων) είναι φανερά μια σημαντική ποσότητα που δηλώνει το πλάτος του υλοκύματος (ή το πλάτος της συμβολής των υλοκυμάτων του συστήματος, αλλά έχει και μια άλλη εφαρμογή: Το τετράγωνό της δίνει τη υλοκυματική πυκνότητα στο χώρα ή αλλιώς την πιθανότητα να εντοπίσουμε το σωματίδιο (ή το αντίστοιχο μάζας του σωματιδίου) σε κάθε σημείο του χώρου. Φυσικά για το σύνολο του χώρου έχουμε:

$\int \psi ^{2}dV=1$

όπου:

V: ο όγκος του χώρου.

Στην περίπτωση που η παραπάνω εξίσωση ισχήει για μια λύση ψ, τότε η λύση ονομάζεται « κανονικοποιημένη ». Αν για οποιοδήποτε λόγο έχουμε μια μη κανονικοποιημένη λύση, τότε είναι πολύ απλό να την κανονικοποιήσουμε, πολλαπλασιάζοντάς την με έναν « παράγοντα κανονικοποίησηης » (N), που υπολογίζεται από την ακόλουθη σχέση:

$N^{-2}=\int \psi ^{2}dV\Leftrightarrow N={\frac {1}{{\begin{pmatrix}\int \psi ^{2}dV\end{pmatrix}}^{2}}}$

Έτσι προκύπτει μια νέα κανονικοποιημένη λύση, ψ₀, για την οποία ισχύει:

$\psi _{0}=N\psi$

Το άτομο του υδρογόνου

Το άτομο του υδρογόνου αποτελείται από ένα πρωτόνιο και ένα ηλεκτρόνιο που περιφέρεται γύρω από αυτό. Είναι ένα απλό και κλασσικό σύστημα δύο σωματιδίων. Θεωρητικά λοιπόν, η εξίσωση Schrödinger για το σύστημα γράφεται:

$H\psi =E\psi$
ή πιο αναλυτικά:
$-{\begin{Bmatrix}{\begin{matrix}2\\\sum \\i=1\end{matrix}}{\begin{bmatrix}{\frac {h^{2}}{8\pi ^{2}m_{i}}}{\nabla _{i}}^{2}+V{\begin{pmatrix}x_{i},y_{i},z_{i}\end{pmatrix}}\end{bmatrix}}\end{Bmatrix}}\psi =E\psi \Leftrightarrow -{\begin{bmatrix}{\frac {h^{2}}{8\pi ^{2}m_{p}}}{\nabla _{p}}^{2}+V{\begin{pmatrix}x_{p},y_{p},z_{p}\end{pmatrix}}+{\frac {h^{2}}{8\pi ^{2}m_{e}}}{\nabla _{e}}^{2}+V{\begin{pmatrix}x_{e},y_{e},z_{e}\end{pmatrix}}\end{bmatrix}}\psi =E\psi$

όπου

${\nabla _{i}}^{2}={\frac {\partial ^{2}}{\partial {x_{i}}^{2}}}+{\frac {\partial ^{2}}{\partial {y_{i}}^{2}}}+{\frac {\partial ^{2}}{\partial {z_{i}}^{2}}}$

όπου

x_p, y_p, z_p: οι καρτεσιανές συντεταγμένες του πρωτονίου στο χώρο.

x_e, y_e, z_e: οι καρτεσιανές συντεταγμένες του ηλεκτρονίου στο χώρο.

m_p: η μάζα του πρωτονίου: $m_{p}=1,67262158\cdot 10^{-28}\;kg$.

m_e: η μάζα του ηλεκτρονίου: $m_{e}=9,1\cdot 10^{-31}\;kg$

• Στην περίπτωση που έχουμε ένα « ισότοπο » του κοινού ¹Η, δηλαδή το D (« δευτέριο »΄) ή το T (« τρίτιο »΄), έχουμε αντίστοιχα m_d ή m_t αντί m_p. Στην πράξη αυτό σημαίνει μεταβολή της κινητικής ενέργειας του πυρήνα. Γι' αυτό τα ισότοπα διαφέρουν μόνο στην « κινητική » των αντιδράσεων,

Επειδή όμως το πρωτόνιο είναι 1836 φορές μικρότερο σε μάζα από το ηλεκτρόνιο, η κίνησή του που επιβάλλεται από την επίδραση του ηλεκτρονίου είναι πολύ μικρότερη σε σχέση με την αντίστοιχη του ηλεκτρονίου, ώστε για ευκολία μας μπορεί να θεωρηθεί ότι είναι κατά προσέγγιση ακίνητο στην αρχή του συστήματος των καρτεσιανών συντεταγμένων. Με αυτήν την προσέγγιση παίρνουμε ως ψ την κυματοσυνάρτηση μόνο του ηλεκτρονίου και τα τροχιακά που προκύπτουν ονομάζονται « ατομικά τροχιακά υδρογόνου ». Στην περίπτωση (παραλείποντας και τους περιττούς πια δείκτες e) αυτή δηλαδή έχουμε:

$H\psi =E\psi$
ή πιο αναλυτικά:
$-{\begin{bmatrix}{\frac {h^{2}}{8\pi ^{2}m}}\nabla ^{2}+{\frac {q^{2}}{4\pi \epsilon _{0}}}{\frac {1}{\sqrt {x^{2}+y^{2}+z^{2}}}}\end{bmatrix}}\psi =E\psi$

όπου

q: Το ηλεκτρικό φορτίου του ηλεκτρονίου: $q=1,60210\cdot 10^{-19}\;Cb$.

ε₀: « Διηλεκτρική σταθερά του κενού »: $\epsilon _{0}\simeq 8,85418\cdot 10^{-12}\;Cb^{2}/Ntm^{2}$.

Διαπιστώνουμε στην παραπάνω σχέση ότι οι καρτεσιανές συντεταγμένες είναι εξαιρετικά άβολες στη διατύπωση ειδικά του όρου της δυναμικής ενέργειας του ηλεκτρονίου: $V{\begin{pmatrix}x,y,z\end{pmatrix}}={\frac {q^{2}}{4\pi \epsilon _{0}}}{\frac {1}{\sqrt {x^{2}+y^{2}+z^{2}}}}$. Είναι καλύτερα να τις μετατρέψουμε σε « σφαιρικές συντεταγμένες », με τις ακόλουθες σχέσεις, που προκύπτουν από την « τριγωνομετρία »:

$x=r\eta \mu \theta \sigma \upsilon \nu \phi$
$y=r\eta \mu \theta \eta \mu \phi$
$z=r\sigma \upsilon \nu \theta$

Τετραγωνίζοντας τις παραπάνω σχέσεις κατά μέλη και στην συνέχεια προσθέτοντας τις σχέσεις που προκύπτουν όλες κατά μέλη, παίρνουμε:

$r^{2}=x^{2}+y^{2}+z^{2}\Leftrightarrow r={\sqrt {x^{2}+y^{2}+z^{2}}}$

Με τις παραπάνω σχέσεις μετατροπής σε σφαιρικές συντεταγμένες ο όρος της δυναμικής ενέργειας του ηλεκτρονίου στην ατομική εξίσωση Schrödinger για το υδρογόνο απλοποιείται δραστικά και γίνεται:

$V=-{\frac {q^{2}}{4\pi \epsilon _{0}}}{\frac {1}{r}}$ Βέβαια, ο όρος της κινητικής ενέργειας πολυκλοποιείται και γίνεται:

$\nabla ^{2}={\frac {1}{r^{2}}}{\begin{bmatrix}{\frac {\partial }{\partial r}}{\begin{pmatrix}r^{2}{\frac {\partial }{\partial r}}\end{pmatrix}}+{\frac {1}{\eta \mu ^{2}\theta }}{\frac {\partial ^{2}}{\partial \phi ^{2}}}+{\frac {1}{\eta \mu \theta }}{\frac {\partial }{\partial \theta }}{\begin{pmatrix}\eta \mu \theta {\frac {\partial }{\partial \theta }}\end{pmatrix}}\end{bmatrix}}$ Με βάση τα παραπάνω, η ατομική εξίσωση Schrödinger για το υδρογόνο σε πολικές συντεταγμένες γίνεται τελικά:

$-{\frac {h^{2}}{8\pi ^{2}mr^{2}}}{\begin{bmatrix}{\frac {\partial }{\partial r}}{\begin{pmatrix}r^{2}{\frac {\partial \psi }{\partial r}}\end{pmatrix}}+{\frac {1}{\eta \mu ^{2}\theta }}{\frac {\partial ^{2}\psi }{\partial \phi ^{2}}}+{\frac {1}{\eta \mu \theta }}{\frac {\partial }{\partial \theta }}{\begin{pmatrix}\eta \mu \theta {\frac {\partial \psi }{\partial \theta }}\end{pmatrix}}\end{bmatrix}}-{\frac {q^{2}}{4\pi \epsilon _{0}r}}\psi =E\psi \Leftrightarrow {\frac {\partial }{\partial r}}{\begin{pmatrix}r^{2}{\frac {\partial \psi }{\partial r}}\end{pmatrix}}+{\frac {1}{\eta \mu ^{2}\theta }}{\frac {\partial ^{2}\psi }{\partial \phi ^{2}}}+{\frac {1}{\eta \mu \theta }}{\frac {\partial }{\partial \theta }}{\begin{pmatrix}\eta \mu \theta {\frac {\partial \psi }{\partial \theta }}\end{pmatrix}}+{\frac {2\pi mq^{2}r}{h^{2}\epsilon _{0}}}\psi =-{\frac {8\pi ^{2}mr^{2}}{h^{2}}}E\psi$

Παρά το γεγονός ότι φαινομενικά η εξίσωση έγινε περισσότερο πολύπλοκη, στην πραγματικότητα έτσι διευκολύνεται η λύση της. Αποδεικνύεται λοιπόν ότι για κάθε λύση της ψ(r,θ,φ} ισχύει:

$\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}=R{\begin{pmatrix}r\end{pmatrix}}Y{\begin{pmatrix}\theta ,\phi \end{pmatrix}}=R{\begin{pmatrix}r\end{pmatrix}}\Theta {\begin{pmatrix}\theta \end{pmatrix}}\Phi {\begin{pmatrix}\phi \end{pmatrix}}$

Τα « ατομικά τροχιακά » που παράγονται από τις παραπάνω εξισώσεις καθορίζονται από τους 4 « κβαντικούς αριθμούς », n, $\ell$, m και m_s:

Ο « κύριος κβαντικός αριθμός » n, παίρνει τιμές: 1, 2, 3,... 7. Θεωρητικά προβλέπονται και μεγαλύτεροι, αλλά n = 7 είναι η μεγαλύτερη τιμή που εμφανίζεται στα γνωστά χημικά στοιχεία.

Ο κβαντικός αριθμός $\ell$ παίρνει τιμές: 0, 1, 2,..., n-1.

Ο κβαντικός αριθμός m παίρνει τιμές: 0, ±1, ±2,..., ±$\ell$.

O κβαντικός αριθμός m_s (σπιν) παίρνει τιμές: ±½.

Οι εξισώσεις των συνηθισμένων ατομικών τροχιακών είναι:

1s: n=1, $\ell$=0: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{\sqrt {\pi }}}e^{-\rho }$, όπου $\rho ={\frac {r}{\alpha _{0}}}$, με $\alpha _{0}={\frac {h^{2}\epsilon _{0}}{\pi m_{e}{q_{e}}^{2}}}$ « ακτίνα Bohr ». 1s¹, δηλαδή το ηλεκτρόνιο στο 1s τροχιακό είναι η βασική κατάσταση για το άτομο του υδρογόνου. Οι παρακάτω είναι διεγερμένες καταστάσεις, δηλαδή προκύπτουν μετά την πρόσληψη κατάλληλης ενέργειας, την οποία΄κανονικά σύντομα θα επανεκπέμψουν σε ακτινοβολία με συχνότητα $v=\Delta E/h$.

2s: n=2, $\ell$=0: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{4{\sqrt {2\pi }}}}{\begin{pmatrix}2-\rho \end{pmatrix}}e^{-{\frac {\rho }{2}}}$.

2p_x: n=2, $\ell$=1: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{4{\sqrt {2\pi }}}}re^{-{\frac {\rho }{2}}}\eta \mu \theta \sigma \upsilon \nu \phi$.

2p_y: n=2, $\ell$=1: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{4{\sqrt {2\pi }}}}re^{-{\frac {\rho }{2}}}\eta \mu \theta \eta \mu \phi$.

2p_z: n=2, $\ell$=1: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{4{\sqrt {2\pi }}}}re^{-{\frac {\rho }{2}}}\sigma \upsilon \nu \phi$.

3s: n=3, $\ell$=0: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{81{\sqrt {3\pi }}}}{\begin{pmatrix}27-18\rho +2\rho ^{2}\end{pmatrix}}e^{-{\frac {\rho }{3}}}$.

3p_x: n=3, $\ell$=1: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {2}{81{\sqrt {2\pi }}}}r{\begin{pmatrix}6-\rho \end{pmatrix}}e^{-{\frac {\rho }{3}}}\eta \mu \theta \sigma \upsilon \nu \phi$.

3p_y: n=3, $\ell$=1: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {2}{81{\sqrt {2\pi }}}}r{\begin{pmatrix}6-\rho \end{pmatrix}}e^{-{\frac {\rho }{3}}}\eta \mu \theta \eta \mu \phi$.

3p_z: n=3, $\ell$=1: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {2}{81{\sqrt {2\pi }}}}r{\begin{pmatrix}6-\rho \end{pmatrix}}e^{-{\frac {\rho }{3}}}\sigma \upsilon \nu \phi$.

3d_z²: n=3, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{81{\sqrt {6\pi }}}}r^{2}e^{-{\frac {\rho }{3}}}{\begin{pmatrix}3\sigma \upsilon \nu ^{2}\theta -1\end{pmatrix}}$.

3d_zx: n=3, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {2}}{81{\sqrt {\pi }}}}r^{2}e^{-{\frac {\rho }{3}}}\eta \mu \theta \sigma \upsilon \nu \theta \sigma \upsilon \nu \phi$.

3d_yz: n=3, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {2}}{81{\sqrt {\pi }}}}r^{2}e^{-{\frac {\rho }{3}}}\eta \mu \theta \sigma \upsilon \nu \theta \eta \mu \phi$.

3d_x²-y²: n=3, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{81{\sqrt {2\pi }}}}\rho ^{2}e^{-{\frac {\rho }{3}}}\eta \mu ^{2}\theta \sigma \upsilon \nu {\begin{pmatrix}2\phi \end{pmatrix}}$.

3d_xy: n=3, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {2}}{81{\sqrt {\pi }}}}\rho ^{2}e^{-{\frac {\rho }{3}}}\eta \mu ^{2}\theta \sigma \upsilon \nu \phi \eta \mu \phi$.

4s: n=4, $\ell$=0: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{1536{\sqrt {\pi }}}}{\begin{pmatrix}192-144\rho +24\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{4}}}$.

4p_x: n=4, $\ell$=1: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{256{\sqrt {5\pi }}}}r{\begin{pmatrix}80-20\rho -\rho ^{2}\end{pmatrix}}e^{-{\frac {\rho }{4}}}\eta \mu \theta \sigma \upsilon \nu \phi$.

4p_y: n=4, $\ell$=1: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{256{\sqrt {5\pi }}}}r{\begin{pmatrix}80-20\rho -\rho ^{2}\end{pmatrix}}e^{-{\frac {\rho }{4}}}\eta \mu \theta \eta \mu \phi$.

4p_z: n=4, $\ell$=1: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{256{\sqrt {5\pi }}}}r{\begin{pmatrix}80-20\rho -\rho ^{2}\end{pmatrix}}e^{-{\frac {\rho }{4}}}\sigma \upsilon \nu \phi$.

4d_z²: n=4, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{3.072{\sqrt {\pi }}}}r^{2}{\begin{pmatrix}12-\rho \end{pmatrix}}e^{-{\frac {\rho }{4}}}{\begin{pmatrix}3\sigma \upsilon \nu ^{2}\theta -1\end{pmatrix}}$.

4d_zx: n=4, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{1.536{\sqrt {\pi }}}}r^{2}{\begin{pmatrix}12-\rho \end{pmatrix}}e^{-{\frac {\rho }{4}}}\eta \mu \theta \sigma \upsilon \nu \theta \sigma \upsilon \nu \phi$.

4d_yz: n=4, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{1.536{\sqrt {\pi }}}}r^{2}{\begin{pmatrix}12-\rho \end{pmatrix}}e^{-{\frac {\rho }{4}}}\eta \mu \theta \sigma \upsilon \nu \theta \eta \mu \phi$.

4d_x²-y²: n=4, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{1.536{\sqrt {\pi }}}}r^{2}{\begin{pmatrix}12-\rho \end{pmatrix}}e^{-{\frac {\rho }{4}}}\eta \mu ^{2}\theta \sigma \upsilon \nu {\begin{pmatrix}2\phi \end{pmatrix}}$.

4d_xy: n=4, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{1.536{\sqrt {\pi }}}}r^{2}{\begin{pmatrix}12-\rho \end{pmatrix}}e^{-{\frac {\rho }{4}}}\eta \mu ^{2}\theta \sigma \upsilon \nu \phi \eta \mu \phi$.

4f_x³: n=4, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{3.072{\sqrt {5\pi }}}}r^{3}e^{-{\frac {\rho }{4}}}{\begin{pmatrix}5\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -3\end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi$.

4f_y³: n=4, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{3.072{\sqrt {5\pi }}}}r^{3}e^{-{\frac {\rho }{4}}}{\begin{pmatrix}5\eta \mu ^{2}\theta \eta \mu ^{2}\phi -3\end{pmatrix}}\eta \mu \theta \eta \mu \phi$.

4f_z³: n=4, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{3.072{\sqrt {5\pi }}}}r^{3}e^{-{\frac {\rho }{4}}}{\begin{pmatrix}5\sigma \upsilon \nu ^{2}\theta -3\end{pmatrix}}\sigma \upsilon \nu \theta$.

4f_x(z²-y²): n=4, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{3.072{\sqrt {\pi }}}}r^{3}e^{-{\frac {\rho }{4}}}{\begin{pmatrix}\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi$.

4f_y(z²-x²): n=4, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{3.072{\sqrt {\pi }}}}r^{3}e^{-{\frac {\rho }{4}}}{\begin{pmatrix}\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi \end{pmatrix}}\eta \mu \theta \eta \mu \phi$.

4f_z(x²-y²): n=4, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{3.072{\sqrt {\pi }}}}r^{3}e^{-{\frac {\rho }{4}}}{\begin{pmatrix}1-2\eta \mu ^{2}\phi \end{pmatrix}}\sigma \upsilon \nu \theta \eta \mu ^{2}\theta$.

4f_xyz: n=4, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{1536{\sqrt {\pi }}}}r^{3}e^{-{\frac {\rho }{4}}}\sigma \upsilon \nu \theta \eta \mu ^{2}\theta \sigma \upsilon \nu \phi \eta \mu \phi$.

5s: n=5, $\ell$=0: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{46.875{\sqrt {5\pi }}}}{\begin{pmatrix}18.750-15.000\rho +3.000\rho ^{2}-200\rho ^{3}+4\rho ^{4}\end{pmatrix}}e^{-{\frac {\rho }{5}}}$.

5p_x: n=5, $\ell$=1: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{46.875{\sqrt {10\pi }}}}r{\begin{pmatrix}7.500-2.250\rho +180\rho ^{2}-4\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{5}}}\eta \mu \theta \sigma \upsilon \nu \phi$.

5p_y: n=5, $\ell$=1: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{46.875{\sqrt {10\pi }}}}r{\begin{pmatrix}7.500-2.250\rho +180\rho ^{2}-4\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{5}}}\eta \mu \theta \eta \mu \phi$.

5p_z: n=5, $\ell$=1: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{46.875{\sqrt {10\pi }}}}r{\begin{pmatrix}7.500-2.250\rho +180\rho ^{2}-4\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{5}}}\sigma \upsilon \nu \theta$.

5d_z²: n=5, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{46.875{\sqrt {35\pi }}}}r^{2}{\begin{pmatrix}525-70\rho +2\rho ^{2}\end{pmatrix}}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}3\sigma \upsilon \nu ^{2}\theta -1\end{pmatrix}}$.

5d_zx: n=5, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {2{\sqrt {3}}}{46.875{\sqrt {14\pi }}}}r^{2}{\begin{pmatrix}525-70\rho +2\rho ^{2}\end{pmatrix}}e^{-{\frac {\rho }{5}}}\eta \mu \theta \sigma \upsilon \nu \theta \sigma \upsilon \nu \phi$.

5d_yz: n=5, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {2{\sqrt {3}}}{46.875{\sqrt {14\pi }}}}r^{2}{\begin{pmatrix}525-70\rho +2\rho ^{2}\end{pmatrix}}e^{-{\frac {\rho }{5}}}\eta \mu \theta \sigma \upsilon \nu \theta \eta \mu \phi$.

5d_x²-y²: n=5, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{46875{\sqrt {14\pi }}}}r^{2}{\begin{pmatrix}525-70\rho +2\rho ^{2}\end{pmatrix}}e^{-{\frac {\rho }{5}}}\eta \mu ^{2}\theta \sigma \upsilon \nu {\begin{pmatrix}2\phi \end{pmatrix}}$.

5d_xy: n=5, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {2{\sqrt {3}}}{46.875{\sqrt {14\pi }}}}r^{2}{\begin{pmatrix}525-70\rho +2\rho ^{2}\end{pmatrix}}e^{-{\frac {\rho }{5}}}\eta \mu ^{2}\theta \sigma \upsilon \nu \phi \eta \mu \phi$.

5f_x³: n=5, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{46.875{\sqrt {10\pi }}}}r^{3}{\begin{pmatrix}20-\rho \end{pmatrix}}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}5\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -3\end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi$.

5f_y³: n=5, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{46.875{\sqrt {10\pi }}}}r^{3}{\begin{pmatrix}20-\rho \end{pmatrix}}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}5\eta \mu ^{2}\theta \eta \mu ^{2}\phi -3\end{pmatrix}}\eta \mu \theta \eta \mu \phi$.

5f_z³: n=5, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{46.875{\sqrt {10\pi }}}}r^{3}{\begin{pmatrix}20-\rho \end{pmatrix}}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}5\sigma \upsilon \nu ^{2}\theta -3\end{pmatrix}}\sigma \upsilon \nu \theta$.

5f_x(z²-y²): n=5, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{46.875{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}20-\rho \end{pmatrix}}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi$.

5f_y(z²-x²): n=5, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{46.875{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}20-\rho \end{pmatrix}}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi \end{pmatrix}}\eta \mu \theta \eta \mu \phi$.

5f_z(x²-y²): n=5, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{46.875{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}20-\rho \end{pmatrix}}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}1-2\eta \mu ^{2}\phi \end{pmatrix}}\sigma \upsilon \nu \theta \eta \mu ^{2}\theta$.

5f_xyz: n=5, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {2{\sqrt {3}}}{46875{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}20-\rho \end{pmatrix}}e^{-{\frac {\rho }{5}}}\sigma \upsilon \nu \theta \eta \mu ^{2}\theta \sigma \upsilon \nu \phi \eta \mu \phi$.

5g_z⁴: n=5, $\ell$=4: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{28.800{\sqrt {70\pi }}}}r^{4}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}35\sigma \upsilon \nu ^{4}\theta -30\sigma \upsilon \nu ^{2}\theta +3\end{pmatrix}}$, όπου k γινόμενο σταθερών.

5g_z²x: n=5, $\ell$=4: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{28.800{\sqrt {70\pi }}}}r^{4}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}4\sigma \upsilon \nu ^{2}\theta -3\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -3\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi \sigma \upsilon \nu \theta$.

5g_z²y: n=5, $\ell$=4: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{28.800{\sqrt {70\pi }}}}r^{4}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}4\sigma \upsilon \nu ^{2}\theta -3\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -3\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}\eta \mu \theta \eta \mu \phi \sigma \upsilon \nu \theta$.

5g_z²xy: n=5, $\ell$=4: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{28.800{\sqrt {70\pi }}}}r^{4}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}6\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}\eta \mu ^{2}\theta \eta \mu \phi \sigma \upsilon \nu \phi$.

5g_z²(x²-y²): n=5, $\ell$=4: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{28.800{\sqrt {70\pi }}}}r^{4}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}6\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}{\begin{pmatrix}1-2\eta \mu ^{2}\phi \end{pmatrix}}\eta \mu ^{2}\theta$.

5g_zx³: n=5, $\ell$=4: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{28.800{\sqrt {70\pi }}}}r^{4}e^{-{\frac {\rho }{5}}}\eta \mu ^{3}\theta \sigma \upsilon \nu \phi \sigma \upsilon \nu \theta {\begin{pmatrix}1-4\eta \mu ^{2}\phi \end{pmatrix}}$.

5g_zy³: n=5, $\ell$=4: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{28.800{\sqrt {70\pi }}}}r^{4}e^{-{\frac {\rho }{5}}}\eta \mu ^{3}\theta \eta \mu \phi \sigma \upsilon \nu \theta {\begin{pmatrix}3-4\eta \mu ^{2}\phi \end{pmatrix}}$.

5g_xy(x²-y²): n=5, $\ell$=4: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{28.800{\sqrt {70\pi }}}}r^{4}e^{-{\frac {\rho }{5}}}\eta \mu ^{3}\theta \sigma \upsilon \nu \phi \sigma \upsilon \nu \theta {\begin{pmatrix}1-2\eta \mu ^{2}\phi \end{pmatrix}}$.

5g_x⁴+y⁴: n=5, $\ell$=4: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{28.800{\sqrt {70\pi }}}}r^{4}e^{-{\frac {\rho }{5}}}\eta \mu ^{4}\theta {\begin{pmatrix}1-4\sigma \upsilon \nu ^{2}\phi \eta \mu ^{2}\phi \end{pmatrix}}$.

6s: n=6, $\ell$=0: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{1.049.760{\sqrt {6\pi }}}}{\begin{pmatrix}174.960-145.800\rho +32.400\rho ^{2}-2.700\rho ^{3}+90\rho ^{4}-\rho ^{5}\end{pmatrix}}e^{-{\frac {\rho }{6}}}$.

6p_x: n=6, $\ell$=1: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{12.186{\sqrt {70\pi }}}}r{\begin{pmatrix}5.506.240-1.870.830\rho +183.708\rho ^{2}-6.804\rho ^{3}+81\rho ^{4}\end{pmatrix}}e^{-{\frac {\rho }{6}}}\eta \mu \theta \sigma \upsilon \nu \phi$.

6p_y: n=6, $\ell$=1: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{12.186{\sqrt {70\pi }}}}r{\begin{pmatrix}5.506.240-1.870.830\rho +183.708\rho ^{2}-6.804\rho ^{3}+81\rho ^{4}\end{pmatrix}}e^{-{\frac {\rho }{6}}}\eta \mu \theta \eta \mu \phi$.

6p_z: n=6, $\ell$=1: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{12.186{\sqrt {70\pi }}}}r{\begin{pmatrix}5.506.240-1.870.830\rho +183.708\rho ^{2}-6.804\rho ^{3}+81\rho ^{4}\end{pmatrix}}e^{-{\frac {\rho }{6}}}\sigma \upsilon \nu \theta$.

6d_z²: n=6, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{839.808{\sqrt {21\pi }}}}r^{2}{\begin{pmatrix}9.072-1.512\rho +72\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}3\sigma \upsilon \nu ^{2}\theta -1\end{pmatrix}}$.

6d_zx: n=6, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{419.904{\sqrt {35\pi }}}}r^{2}{\begin{pmatrix}9.072-1.512\rho +72\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{6}}}\eta \mu \theta \sigma \upsilon \nu \theta \sigma \upsilon \nu \phi$.

6d_yz: n=6, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{419.904{\sqrt {35\pi }}}}r^{2}{\begin{pmatrix}9.072-1.512\rho +72\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{6}}}\eta \mu \theta \sigma \upsilon \nu \theta \eta \mu \phi$.

6d_x²-y²: n=6, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{839.808{\sqrt {35\pi }}}}r^{2}{\begin{pmatrix}9.072-1.512\rho +72\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{6}}}\eta \mu ^{2}\theta \sigma \upsilon \nu {\begin{pmatrix}2\phi \end{pmatrix}}$.

6d_xy: n=6, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{419.904{\sqrt {35\pi }}}}r^{2}{\begin{pmatrix}9.072-1.512\rho +72\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}5\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -3\end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi$.

6f_x³: n=6, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{97.200{\sqrt {10\pi }}}}r^{3}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}5\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -3\end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi$.

6f_y³: n=6, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{97.200{\sqrt {10\pi }}}}r^{3}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}5\eta \mu ^{2}\theta \eta \mu ^{2}\phi -3\end{pmatrix}}\eta \mu \theta \eta \mu \phi$.

6f_z³: n=6, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{97.200{\sqrt {10\pi }}}}r^{3}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}5\sigma \upsilon \nu ^{2}\theta -3\end{pmatrix}}\sigma \upsilon \nu \theta$.

6f_x(z²-y²): n=6, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{97.200{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi$.

6f_y(z²-x²): n=6, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{97.200{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi \end{pmatrix}}\eta \mu \theta \eta \mu \phi$.

6f_z(x²-y²): n=6, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{97.200{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}1-2\eta \mu ^{2}\phi \end{pmatrix}}\sigma \upsilon \nu \theta \eta \mu ^{2}\theta$.

6f_xyz: n=6, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{194.400{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}\sigma \upsilon \nu \theta \eta \mu ^{2}\theta \sigma \upsilon \nu \phi \eta \mu \phi$.

6g_z⁴: n=6, $\ell$=4: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{457.400{\sqrt {70\pi }}}}r^{4}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}35\sigma \upsilon \nu ^{4}\theta -30\sigma \upsilon \nu ^{2}\theta +3\end{pmatrix}}$, όπου k γινόμενο σταθερών.

6g_z²x: n=6, $\ell$=4: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{457.400{\sqrt {70\pi }}}}r^{4}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}4\sigma \upsilon \nu ^{2}\theta -3\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -3\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi \sigma \upsilon \nu \theta$.

6g_z²y: n=6, $\ell$=4: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{457.400{\sqrt {70\pi }}}}r^{4}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}4\sigma \upsilon \nu ^{2}\theta -3\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -3\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}\eta \mu \theta \eta \mu \phi \sigma \upsilon \nu \theta$.

6g_z²xy: n=6, $\ell$=4: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{457.400{\sqrt {70\pi }}}}r^{4}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}6\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}\eta \mu ^{2}\theta \eta \mu \phi \sigma \upsilon \nu \phi$.

6g_z²(x²-y²): n=6, $\ell$=4: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{457.400{\sqrt {70\pi }}}}r^{4}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}6\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}{\begin{pmatrix}1-2\eta \mu ^{2}\phi \end{pmatrix}}\eta \mu ^{2}\theta$.

6g_zx³: n=6, $\ell$=4: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{457.400{\sqrt {70\pi }}}}r^{4}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}\eta \mu ^{3}\theta \sigma \upsilon \nu \phi \sigma \upsilon \nu \theta {\begin{pmatrix}1-4\eta \mu ^{2}\phi \end{pmatrix}}$.

6g_zy³: n=6, $\ell$=4: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{457.400{\sqrt {70\pi }}}}r^{4}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}\eta \mu ^{3}\theta \eta \mu \phi \sigma \upsilon \nu \theta {\begin{pmatrix}3-4\eta \mu ^{2}\phi \end{pmatrix}}$.

6g_xy(x²-y²): n=6, $\ell$=4: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{457.400{\sqrt {70\pi }}}}r^{4}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}\eta \mu ^{3}\theta \sigma \upsilon \nu \phi \sigma \upsilon \nu \theta {\begin{pmatrix}1-2\eta \mu ^{2}\phi \end{pmatrix}}$.

6g_x⁴+y⁴: n=6, $\ell$=4: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{457.400{\sqrt {70\pi }}}}r^{4}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}\eta \mu ^{4}\theta {\begin{pmatrix}1-4\sigma \upsilon \nu ^{2}\phi \eta \mu ^{2}\phi \end{pmatrix}}$.

7s: n=7, $\ell$=0: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{117.649k{\sqrt {\pi }}}}{\begin{pmatrix}296.475.480-254.121.408\rho +60.505.200\rho ^{2}-5.762.400\rho ^{3}+246.960\rho ^{4}-4.704\rho ^{5}+32\rho ^{6}\end{pmatrix}}e^{-{\frac {\rho }{7}}}$.

7p_x: n=7, $\ell$=1: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{117.649k{\sqrt {\pi }}}}r{\begin{pmatrix}112.943.040-40.336.800\rho +4.609.920\rho ^{2}-164.640\rho ^{3}+4.480\rho ^{4}-32\rho ^{5}\end{pmatrix}}e^{-{\frac {\rho }{7}}}\eta \mu \theta \sigma \upsilon \nu \phi$.

7p_y: n=7, $\ell$=1: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{117.649k{\sqrt {\pi }}}}r{\begin{pmatrix}112.943.040-40.336.800\rho +4.609.920\rho ^{2}-164.640\rho ^{3}+4.480\rho ^{4}-32\rho ^{5}\end{pmatrix}}e^{-{\frac {\rho }{7}}}\eta \mu \theta \eta \mu \phi$.

7p_z: n=7, $\ell$=1: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{117.649k{\sqrt {\pi }}}}r{\begin{pmatrix}112.943.040-40.336.800\rho +4.609.920\rho ^{2}-164.640\rho ^{3}+4.480\rho ^{4}-32\rho ^{5}\end{pmatrix}}e^{-{\frac {\rho }{7}}}\sigma \upsilon \nu \theta$.

7d_z²: n=7, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{453.789{\sqrt {21\pi }}}}r^{2}{\begin{pmatrix}14.406-2.958\rho +84\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{7}}}{\begin{pmatrix}3\sigma \upsilon \nu ^{2}\theta -1\end{pmatrix}}$.

7d_zx: n=7, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{453.789{\sqrt {7\pi }}}}r^{2}{\begin{pmatrix}14.406-2.958\rho +84\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{7}}}\eta \mu \theta \sigma \upsilon \nu \theta \sigma \upsilon \nu \phi$.

7d_yz: n=7, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{453.789{\sqrt {7\pi }}}}r^{2}{\begin{pmatrix}14.406-2.958\rho +84\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{7}}}\eta \mu \theta \sigma \upsilon \nu \theta \eta \mu \phi$.

7d_x²-y²: n=7, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{907.578{\sqrt {7\pi }}}}r^{2}{\begin{pmatrix}14.406-2.958\rho +84\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{7}}}\eta \mu ^{2}\theta \sigma \upsilon \nu {\begin{pmatrix}2\phi \end{pmatrix}}$.

7d_xy: n=7, $\ell$=2: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{453.789{\sqrt {7\pi }}}}r^{2}{\begin{pmatrix}14.406-2.958\rho +84\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{7}}}{\begin{pmatrix}5\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -3\end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi$.

7f_x³: n=7, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{180.075{\sqrt {10\pi }}}}r^{3}{\begin{pmatrix}28-\rho \end{pmatrix}}e^{-{\frac {\rho }{7}}}{\begin{pmatrix}5\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -3\end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi$.

7f_y³: n=7, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{180.075{\sqrt {10\pi }}}}r^{3}{\begin{pmatrix}28-\rho \end{pmatrix}}e^{-{\frac {\rho }{7}}}{\begin{pmatrix}5\eta \mu ^{2}\theta \eta \mu ^{2}\phi -3\end{pmatrix}}\eta \mu \theta \eta \mu \phi$.

7f_z³: n=7, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{180.075{\sqrt {10\pi }}}}r^{3}{\begin{pmatrix}28-\rho \end{pmatrix}}e^{-{\frac {\rho }{7}}}{\begin{pmatrix}5\sigma \upsilon \nu ^{2}\theta -3\end{pmatrix}}\sigma \upsilon \nu \theta$.

7f_x(z²-y²): n=7, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{180.075{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}28-\rho \end{pmatrix}}e^{-{\frac {\rho }{7}}}{\begin{pmatrix}\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi$.

7f_y(z²-x²): n=7, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{180.075{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}28-\rho \end{pmatrix}}e^{-{\frac {\rho }{7}}}{\begin{pmatrix}\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi \end{pmatrix}}\eta \mu \theta \eta \mu \phi$.

7f_z(x²-y²): n=7, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{180.075{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}28-\rho \end{pmatrix}}e^{-{\frac {\rho }{7}}}{\begin{pmatrix}1-2\eta \mu ^{2}\phi \end{pmatrix}}\sigma \upsilon \nu \theta \eta \mu ^{2}\theta$.

7f_xyz: n=7, $\ell$=3: $\psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{360.150{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}28-\rho \end{pmatrix}}e^{-{\frac {\rho }{7}}}\sigma \upsilon \nu \theta \eta \mu ^{2}\theta \sigma \upsilon \nu \phi \eta \mu \phi$.